Skip to main content
Logo image

Integrating WeBWorK into Textbooks Sample Exercises

Robert Beezer, Alex Jordan

Appendix A Hints, Answers, and Solutions

1 Instructive Examples
1.1 Arithmetic

Checkpoint 1.1.1. Adding Single-Digit Integers.

Answer.
\(7\)
🔗
🔗
Solution.
\(6 + 1 = {7}\text{.}\)
🔗
🔗

Checkpoint 1.1.2. Declaring a Problem Seed.

Answer.
\(13\)
🔗
🔗
Solution.
\(5 + 8 = {13}\text{.}\)
🔗
🔗

Checkpoint 1.1.3. Controlling Randomness.

Answer.
\(3\)
🔗
🔗
Solution.
\(1 + 2 = {3}\text{.}\)
🔗
🔗

Checkpoint 1.1.4. Special Answer Checking.

Answer.
\(x^{8}\)
🔗
🔗
Solution.
We add the exponents as follows, while including a gratuitous reference to the quadratic formula:
🔗
\begin{equation*} \begin{aligned} {x^{5}x^{3}}\amp =x^{5+3}\amp \text{Theorem 1.2.1}\\ \amp =x^{8} \end{aligned} \end{equation*}
🔗
🔗

Checkpoint 1.1.5. Using Hints.

Hint.
Factor the number inside the radical.
🔗
🔗
Answer.
\(4\sqrt{3}\)
🔗
🔗
Solution.
\begin{equation*} {\sqrt{48}}=\sqrt{4^2\cdot 3}=4\sqrt{3} \end{equation*}
🔗
🔗

Checkpoint 1.1.6. No Randomization.

Answer.
\(3\)
🔗
🔗

Checkpoint 1.1.7. Local PG.

Answer.
\(6\)
🔗
🔗

Checkpoint 1.1.8. Local PG File.

Answer.
\(4\)
🔗
🔗

1.2 The Quadratic Formula

Checkpoint 1.2.2. Solving Quadratic Equations.

1.2.2.a Identify Coefficients.
Answer 1.
\(2\)
🔗
🔗
Answer 2.
\(-5\)
🔗
🔗
Answer 3.
\(-12\)
🔗
🔗
Solution.
Take the coefficient of \(x^2\) for the value of \(a\text{,}\) the coefficient of \(x\) for \(b\text{,}\) and the constant for \(c\text{.}\) In this case, they are \(a = {2}\text{,}\) \(b = {-5}\text{,}\) \(c = {-12}\text{.}\)
🔗
🔗
1.2.2.b Use the Quadratic Formula.
Answer.
\(\left\{4,\frac{-3}{2}\right\}\)
🔗
🔗
Solution.
Recall that the quadratic formula is given in Theorem 1.2.1.
🔗
You already identified \(a = {2}\text{,}\) \(b = {-5}\text{,}\) and \(c = {-12}\text{,}\) so the results are:
🔗
\begin{equation*} x = {\frac{-\left(-5\right)+\sqrt{\left(-5\right)^{2}-4\cdot 2\cdot \left(-12\right)}}{2\cdot 2}} = {4} \end{equation*}
🔗
or
🔗
\begin{equation*} x = {\frac{-\left(-5\right)-\sqrt{\left(-5\right)^{2}-4\cdot 2\cdot \left(-12\right)}}{2\cdot 2}} = {-{\frac{3}{2}}} \end{equation*}
🔗
🔗

Checkpoint 1.2.3. Nested tasks.

1.2.3.a Identify Coefficients.
1.2.3.a.i
Answer.
\(3\)
🔗
🔗
Solution.
Take the coefficient of \(x^2\) for the value of \(a\text{.}\) In this case, \(a = {3}\text{.}\)
🔗
🔗
1.2.3.a.ii
Answer.
\(-16\)
🔗
🔗
Solution.
Take the coefficient of \(x\) for the value of \(b\text{.}\) In this case, \(b = {-16}\text{.}\)
🔗
🔗
1.2.3.a.iii
Answer.
\(-12\)
🔗
🔗
Solution.
Take the constant term for the value of \(c\text{.}\) In this case, \(c = {-12}\text{.}\)
🔗
🔗
1.2.3.b Use the Quadratic Formula.
Answer.
\(\left\{6,\frac{-2}{3}\right\}\)
🔗
🔗
Solution.
Recall that the quadratic formula is given in Theorem 1.2.1.
🔗
You already identified \(a = {3}\text{,}\) \(b = {-16}\text{,}\) and \(c = {-12}\text{,}\) so the results are:
🔗
\begin{equation*} x = {\frac{-\left(-16\right)+\sqrt{\left(-16\right)^{2}-4\cdot 3\cdot \left(-12\right)}}{2\cdot 3}} = {6} \end{equation*}
🔗
or
🔗
\begin{equation*} x = {\frac{-\left(-16\right)-\sqrt{\left(-16\right)^{2}-4\cdot 3\cdot \left(-12\right)}}{2\cdot 3}} = {-{\frac{2}{3}}} \end{equation*}
🔗
🔗

Checkpoint 1.2.4. Copy a Problem with Tasks.

1.2.4.a Identify Coefficients.
Answer 1.
\(2\)
🔗
🔗
Answer 2.
\(-5\)
🔗
🔗
Answer 3.
\(-25\)
🔗
🔗
Solution.
Take the coefficient of \(x^2\) for the value of \(a\text{,}\) the coefficient of \(x\) for \(b\text{,}\) and the constant for \(c\text{.}\) In this case, they are \(a = {2}\text{,}\) \(b = {-5}\text{,}\) \(c = {-25}\text{.}\)
🔗
🔗
1.2.4.b Use the Quadratic Formula.
Answer.
\(\left\{5,\frac{-5}{2}\right\}\)
🔗
🔗
Solution.
Recall that the quadratic formula is given in Theorem 1.2.1.
🔗
You already identified \(a = {2}\text{,}\) \(b = {-5}\text{,}\) and \(c = {-25}\text{,}\) so the results are:
🔗
\begin{equation*} x = {\frac{-\left(-5\right)+\sqrt{\left(-5\right)^{2}-4\cdot 2\cdot \left(-25\right)}}{2\cdot 2}} = {5} \end{equation*}
🔗
or
🔗
\begin{equation*} x = {\frac{-\left(-5\right)-\sqrt{\left(-5\right)^{2}-4\cdot 2\cdot \left(-25\right)}}{2\cdot 2}} = {-{\frac{5}{2}}} \end{equation*}
🔗
🔗

1.3 Open Problem Library

Checkpoint 1.3.1. Cylinder Volume.

Answer 1.
\(360\pi\ {\rm m^{3}}\)
🔗
🔗
Answer 2.
\(1130.97\ {\rm m^{3}}\)
🔗
🔗
Solution.
We use \(r\) to represent the base’s radius, and \(h\) to represent the cylinder’s height.
🔗
A cylinder’s volume formula is \(V= (\text{base area}) \cdot \text{height}\text{.}\) A cylinder’s base is a circle, with its area formula \(A = \pi r^{2}\text{.}\)
🔗
Putting together these two formulas, we have a cylinder’s volume formula:
🔗
\(\displaystyle{ V= \pi r^{2} h }\)
🔗
Throughout these computations, all quantities have units attached, and we only show them in the final step.
🔗
  1. Using the volume formula, we have:
    🔗
    \(\displaystyle{\begin{aligned} V \amp = \pi r^{2} h \\ \amp = \pi \cdot 6^{2} \cdot 10 \\ \amp = \pi \cdot 360 \\ \amp = 360 \pi \textrm{ m}^3 \end{aligned}}\)
    🔗
    Don’t forget the volume unit \(\textrm{m}^3\text{.}\)
    🔗
    🔗
  2. To find the decimal version, we replace \(\pi\) with its decimal value, and we have:
    🔗
    \(\displaystyle{\begin{aligned}[t] V\amp = 360 \pi \\ \amp \approx 360 \cdot 3.14\ldots \\ \amp \approx {1130.97\ {\rm m^{3}}} \end{aligned}}\)
    🔗
    Don’t forget the volume unit \(\textrm{m}^3\text{.}\)
    🔗
    🔗
🔗
🔗

1.4 Antidifferentiation
1.4.2 WeBWorK Exercises

1.4.2.1. Antiderivatives.

Answer.
\(28.3885180688169\)
🔗
🔗
Solution.
SOLUTION
🔗
\begin{equation*} \begin{array}{rcl} \displaystyle \int_0^{2} (4 e^x+2 \sin x)\, dx \amp =\amp \displaystyle 4 e^x-2 \cos x \Big]_0^{2} \\ \amp =\amp (4 e^{2} - 2 \cos 2) - (4 e^0 - 2 \cos0 ) \\ \amp =\amp 4 e^{2} - 2 \cos 2 - 2 \end{array} \end{equation*}
🔗
🔗

1.4.2.4.

Answer.
\(-\cos\mathopen{}\left(x\right)+C\)
🔗
🔗

1.4.2.6. Show Your Work.

Answer.
\(2x\)
🔗
🔗

1.6 Multiple Choice

Checkpoint 1.6.1. Drop-down/Popup.

Answer.
\(\text{is not}\)
🔗
🔗
Solution.
If \(\sqrt{2}\) were rational, then \(\sqrt{2}=\frac{p}{q}\text{,}\) with \(p\) and \(q\) coprime. But then \(2q^2=p^2\text{.}\) By the Fundamental Theorem of Arithmetic, the power of \(2\) dividing the left side is odd, while the power of \(2\) dividing the right side is even. This is a contradiction, so \(\sqrt{2}\) is not rational.
🔗
🔗

Checkpoint 1.6.2. Choose one.

Answer.
\(\text{The Fundamental ... of Calculus}\)
🔗
🔗
Solution.
The correct answer is The Fundamental ... of Calculus.
🔗
🔗

Checkpoint 1.6.3. Choose a Subset of Options.

Answer.
\(\text{Choice 1, Choice 3, Choice 5}\)
🔗
🔗
Solution.
The correct answer is Choice 1, Choice 3, Choice 5.
🔗
🔗

Checkpoint 1.6.4. Choose a Subset of Options with Automated Labeling.

Answer.
\(\text{A, B, D}\)
🔗
🔗
Solution.
The correct answer is A, B, D.
🔗
🔗

Checkpoint 1.6.5. Choose a Subset of Options with Explicit Labeling.

Answer.
\(\text{SUSHI, TACO, PIZZA}\)
🔗
🔗
Solution.
The correct answer is SUSHI, TACO, PIZZA.
🔗
🔗

1.7 Tables

Checkpoint 1.7.1. Complete this Table.

Answer 1.
\(48\)
🔗
🔗
Answer 2.
\(36\)
🔗
🔗
Answer 3.
\(72\)
🔗
🔗
Answer 4.
\(54\)
🔗
🔗
Solution.
\(\times\) \(8\) \(6\)
\(6\) \(48\) \(36\)
\(9\) \(72\) \(54\)
🔗

1.8 Graphics in Exercises

Checkpoint 1.8.1. A static <latex-image> graph.

Answer.
\(\mathop{\rm C}\nolimits\mathopen{}\left(n+1,2\right)\hbox{ or }\frac{\left(n+1\right)n}{2}\)
🔗
🔗

Checkpoint 1.8.2. A randomized <latex-image> graph.

Answer.
\(24\ {\rm cm^{2}}\)
🔗
🔗

Checkpoint 1.8.3. A <latex-image> graph affected by <latex-image-preamble>.

Answer.
\(-1, 1, 2\)
🔗
🔗

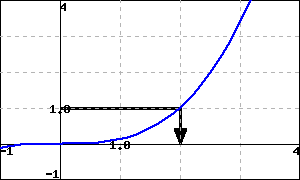
Checkpoint 1.8.5. Solve using a graph.

Answer.
\(\left\{2\right\}\)
🔗
🔗
Solution.
The graph reveals that the solution set to \(f(x)=1\) is \({\left\{2\right\}}\text{.}\)
🔗
a plot of a curve on a cartesian set of axes; the x axis ranges from -1 to 4, and the y-axis ranges from -1 to 4; the curve enters from the left, below the x-axis, and curves upward and to the right until it reaches the point (0,0); from here it continues predominantly rightward for a bit, bending slightly upward more and more as it progresses; it passes through the points (2,1) and (2.51984,2) before leaving the graph moving more and more upward and to the right; a horizontal line segment moves rightward from y=1 on the y-axis until it reaches a point on the curve; a vertical line segment moves down from this point to x=2 on the x-axis.
🔗

Exercises

2 Technical Examples
2.1 PGML Formatting and Verbatim Calisthenics

Checkpoint 2.1.2.

Answer 1.
\({\verb!<>&'";!}\)
🔗
🔗
Answer 2.
\({\verb!#%&<>\^_`|~!}\)
🔗
🔗
Answer 3.
\({\text{\$\{\}}}\)
🔗
🔗
Answer 4.
\(\text{ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789}\)
🔗
🔗
Answer 5.
\({\text{!()*+,-./:=?@[]}}\)
🔗
🔗

2.2 Subject Area Templates

Checkpoint 2.2.1. Answer is a number or a function.

Answer 1.
\(-2\)
🔗
🔗
Answer 2.
\(\frac{7-2x^{7}}{x}\)
🔗
🔗
Solution.
Solution explanation goes here.
🔗
🔗

Checkpoint 2.2.2. Answer is a function with domain issues.

Answer 1.
\(\sqrt{x-4}\)
🔗
🔗
Answer 2.
\(\ln\mathopen{}\left(\left|\frac{x}{x-4}\right|\right)\)
🔗
🔗
Solution.
Solution explanation goes here.
🔗
🔗

Checkpoint 2.2.3. Multiple Choice by Popup, Radio Buttons, or Checkboxes.

Answer 1.
\(\text{Blue}\)
🔗
🔗
Answer 2.
\(\text{Blue}\)
🔗
🔗
Answer 3.
\(\text{Blue}\)
🔗
🔗
Solution.
The correct answer is Blue.
🔗
The correct answer is Blue.
🔗
The correct answer is Blue.
🔗
🔗

Checkpoint 2.2.4.

Answer.
\(\text{Choice 3}\)
🔗
🔗
Solution.
The answer is Choice 3.
🔗
🔗

Checkpoint 2.2.5. Tables.

Answer.
\(5\)
🔗
🔗
Solution.
The missing number is 5.
🔗
🔗

2.3 Stress Tests

Checkpoint 2.3.1. PTX problem source with server-generated images.

2.3.1.a
Solution.
🔗

2.5 Runestone Assignment Testing

Exercises

🔗
PrevTopNext